import numpy as np
import matplotlib.pyplot as plt
from imageio import imread
# Laget for illustrasjon, ikke fullt fungerende
# Bedre, og fungerende, implementasjon i løsningshint 12
class Aritmetisk:
def _encode(self, sequence, length_of_compression, sequences_nr):
compression = np.zeros(sequences_nr)
for j in range(sequences_nr):
c_i = 1
start = 0
for i in range(length_of_compression):
a_i = int(np.round(sequence[j*length_of_compression + i]))
start += self.interval[a_i]*c_i
c_i = self.p[int(a_i)]*c_i
# Here, a number in the interval should be chosen with the smallest bit-length
# This code does't do that and is likely therefore defunct
compression[j] = start
#print(start, start+c_i)
return compression
def encode(self, sequence, length_of_compression):
# We need the number of sequences to be compressed to be integers
assert len(sequence)%length_of_compression == 0
self.length_of_compression = length_of_compression
sequences_nr = int(len(sequence)/length_of_compression)
self.p = np.zeros(256)
for x in sequence:
self.p[int(np.round(x))] += 1
self.p = self.p/len(sequence)
c = np.zeros(256)
c[0] = 0
for i in range(len(self.p)):
c[i] = c[i-1] + self.p[i-1]
self.interval = {i:c[i] for i in range(len(c)) if self.p[i] != 0}
#print(self.interval)
return self._encode(sequence, length_of_compression, sequences_nr)
def decode(self, sequence):
decompressed = list()
for numb in sequence:
start = 0
c_i = 1
for i in range(self.length_of_compression):
a_i = 0
for intens in self.interval:
if numb >= start+(self.interval[intens]*c_i):
a_i = intens
start += self.interval[a_i]*c_i
c_i = self.p[a_i]*c_i
decompressed.append(a_i)
return decompressed
a = Aritmetisk()
compressed = a.encode([1,2,3,3,2, 6,3,2,5,2], 10)
decomp = a.decode(compressed)
print(compressed, decomp)
Litt om forrige forelesning: Kompresjon og koding I¶
Det som skal skje:¶
- Entropi og redundans
- Huffman
- Shannon-Fano
- Aritmetisk
- JPEG: Oblig 2 parafrase
Å forstå entropi¶
Ikke tenk termodynamikk, dette er hentet fra kommunikasjonsteknologi!
Entropi er et mål på hvor mye informasjon en beskjed faktisk inneholder.¶
Litt intuitivt kan vi spør: Hvilket bilde inneholder mest informasjon?

Det er forholdsvis lett å se at Einstein 1 har mindre informasjon enn Einstein 2. I bildebehandling kan vi være matematiske i denne oppfatningen, gjennom entropi.
Og husk: Informasjon er et matematisk begrep som kvantifiserer hvor overraskende / uventet en melding er¶
Om du scannet bildet piksel for piksel, hvor overrasket blir du over den neste pikselen du ser?
For hver melding / symbol / intensitet i gjelder dette: $$ \hbox{info}_i = \log_2{\frac{1}{p[i]}}$$
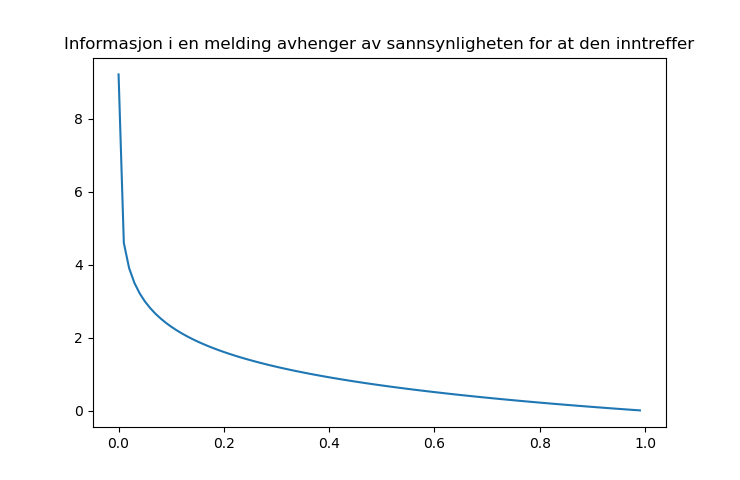
Så nå kan vi regne ut gjennomsnittlig informasjon i en melding / tekst / bilde:¶
p er normalisert histogram.
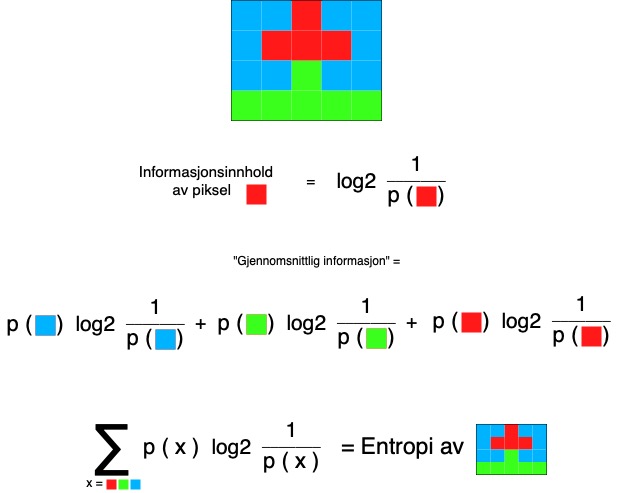
Og dette kan vi bruke til å uttrykke det vi så i de to bildene helt på starten:
| Tegnet-Albert | Albert | |
|---|---|---|
| Entropi | 2.866 | 7.5 |

Interessant, men hva skal vi med det?¶
Entropien vår forteller oss at måten vi representerer den tegnede Albert på er altfor voldsom for hvor lite informasjon den faktisk har i seg. Representasjonen er redundant, og vi kan kode symbolene slik at gjennomsnittlig bit-lengde er nærme entropien, UTEN å miste noe informasjon.
Nytt fagbegrep: Redundans!¶
Det finnes mange former for redundans, men jeg vil vise 2:
- Intersampel redundans
- Psykovisuell redundans
Intersampel redundans:¶
Hva har disse to bildene til felles?
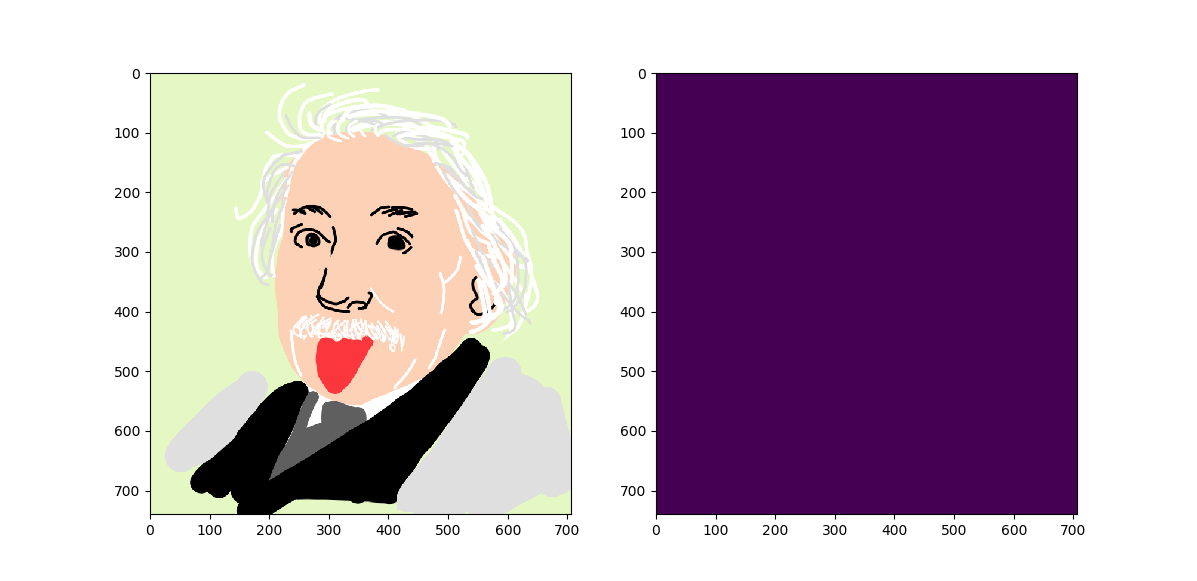
Det lilla bildet kunne vært representert som bredde, høyde, lilla, og ingen informasjon ville vært tapt.
Psykovisuell redundans:¶
Et av disse bildene er komprimert til en $\frac{1}{8}$ av den andres størrelse. Kan du se hvilket?

Hva med nå?

JPEG i oblig 2 bruker dette!
Kompresjonsmetoder¶
Vi skal snakke om 4 denne gangen:
- Huffman
- Shannon-Fano
- Aritmetisk
- JPEG
Jeg vil også vise at kompresjon ofte er en 3-stegs prosess:

Og jeg vil uttrykke hvilket steg vi er på, og også hvilken redundans vi reduserer.
cow = imread("tiny_cow.jpg", as_gray=True)//(2**(8-3))
p = np.zeros(2**3)
for i in cow.ravel():
p[int(i)] += 1
plt.plot(p)
print(p)
print("Filstørrelse:", np.sum(p*3),"bits")
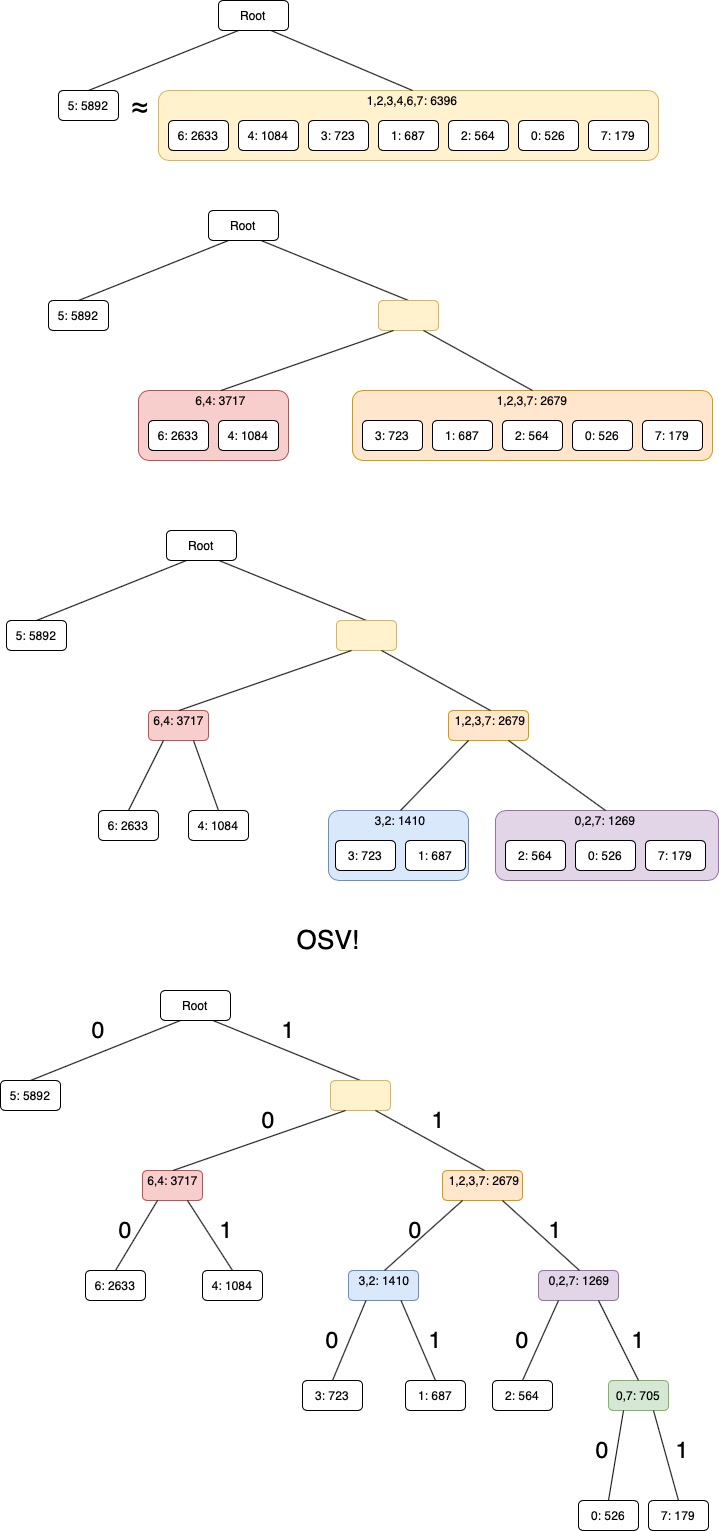
Steg 1: Gro et tre¶
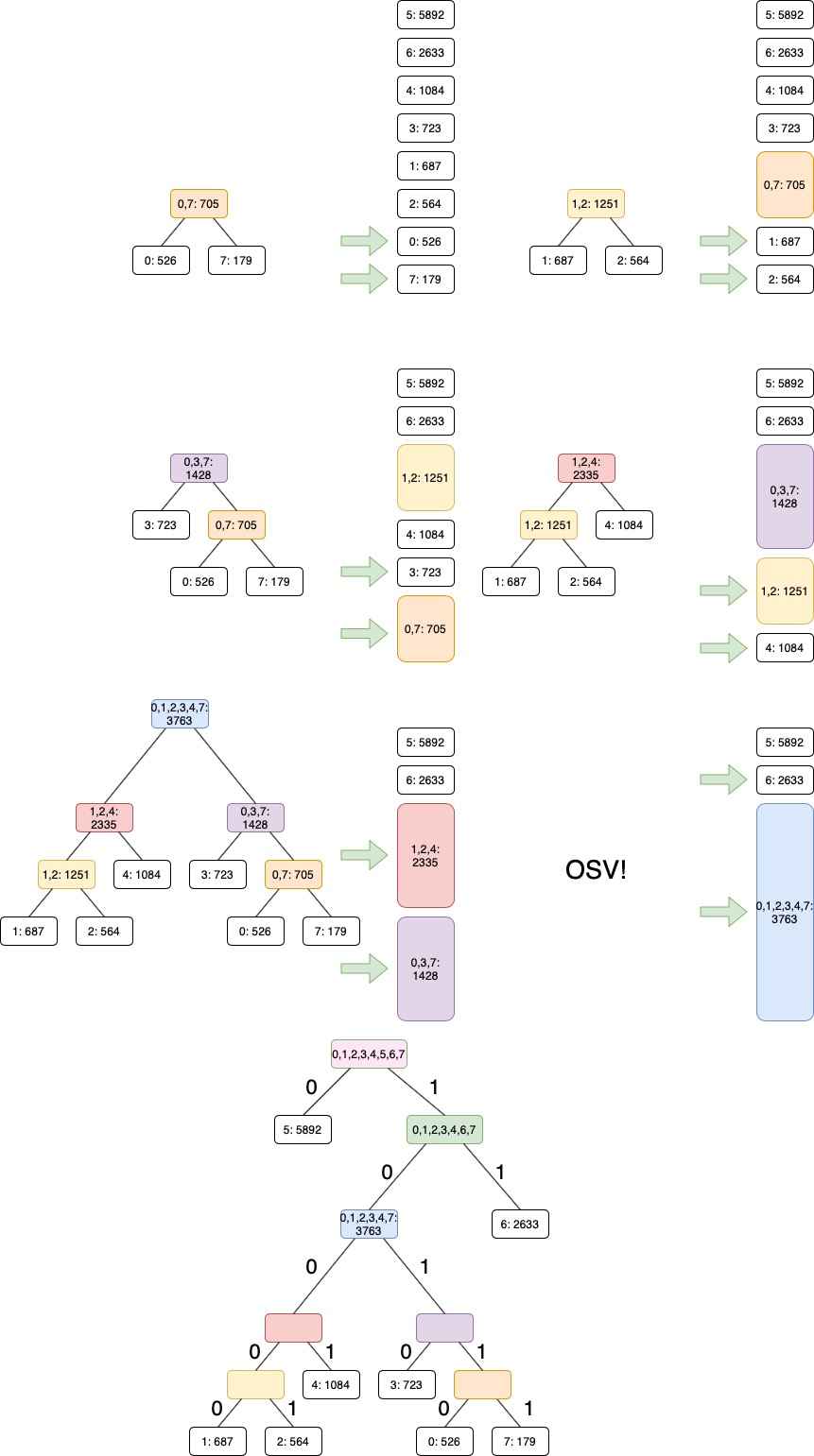
Steg 2: Kodebok¶
| Intensitet | Kode | Bitlengde |
|---|---|---|
| 0 | 10110 | 5 |
| 1 | 10000 | 5 |
| 2 | 10001 | 5 |
| 3 | 1010 | 4 |
| 4 | 1001 | 4 |
| 5 | 0 | 1 |
| 6 | 11 | 2 |
| 7 | 10111 | 5 |
Steg 2: Kodebok¶
| Intensitet | Kode | Bitlengde |
|---|---|---|
| 0 | 11110 | 5 |
| 1 | 1101 | 4 |
| 2 | 1110 | 4 |
| 3 | 1100 | 4 |
| 4 | 101 | 3 |
| 5 | 0 | 1 |
| 6 | 100 | 3 |
| 7 | 11111 | 5 |
Hvem vant?¶
Ny kodelengde vil bli histogram[i] * bit_lengde_i for hver intensitet:
| Representasjonslengde | Bitlengde | |
|---|---|---|
| Huffman | 28166.0 bits | 2.292155 |
| Shannon-Fano | 28464.0 bits | 2.316406 |
| Entropi | 27700.7984439388 | 2.254297 |
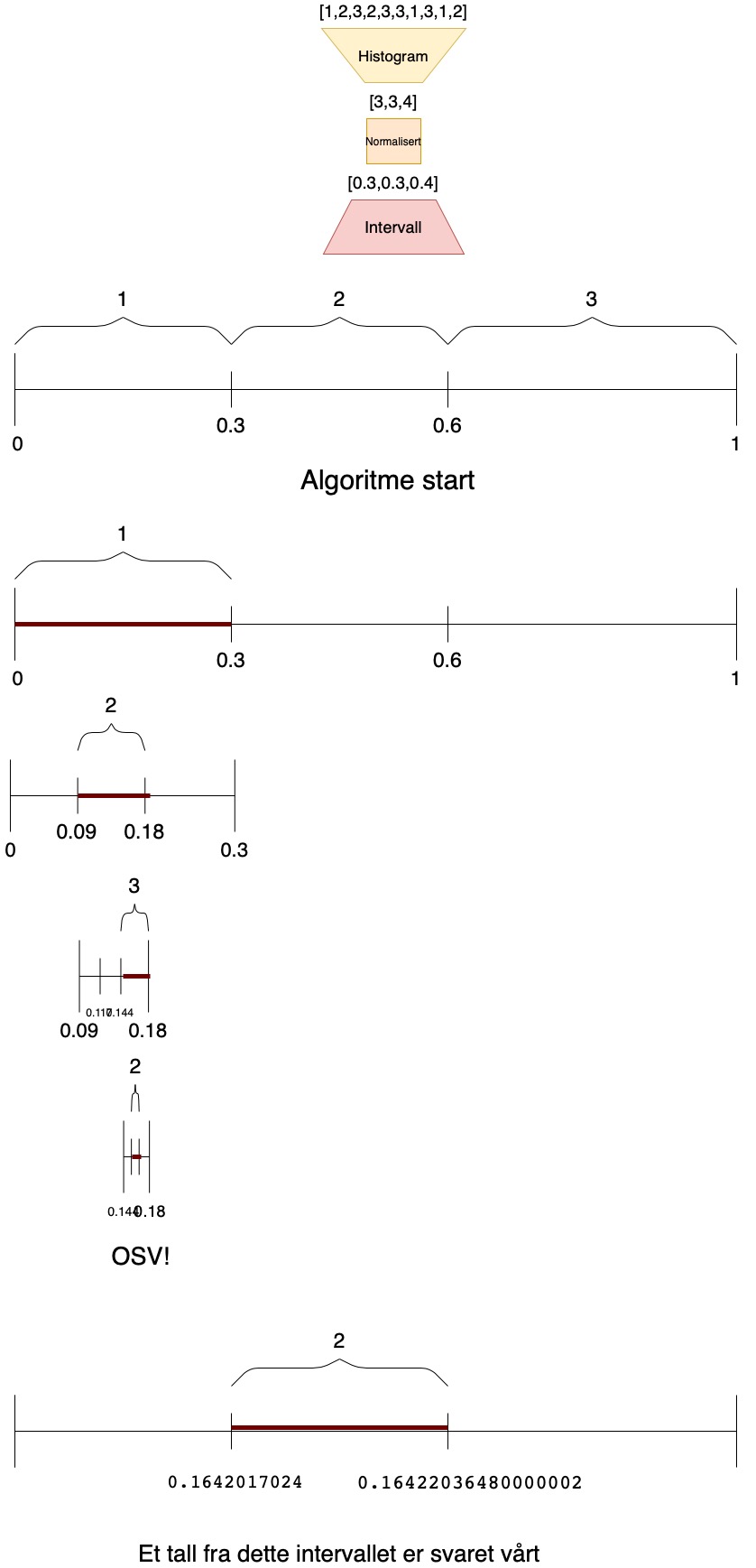
sek = [1,2,3,2,3,3,1,3,1,2]
a = Aritmetisk()
compressed = a.encode(sek, len(sek))
reconstruct = a.decode(compressed)
print("Komprimert:",compressed[0])
print("Rekonstruert:", reconstruct)
Under var et eksempel på aritmetisk koding som førte til tap, der årsaken muligens er at et ikke-optimalt tall hadde blitt valgt fra intervallet. Man burde ikke velge et vilkårlig tall, man burde ta et tall med minst mulig bit-representasjon.
cow_int = cow.astype(int)
compressed = a.encode(cow_int.ravel(), int(cow_int.shape[1]/8))
decomp = a.decode(compressed)
plt.imshow(cow_int, cmap="gray")
plt.title("Original")
plt.figure()
plt.imshow(np.array(decomp).reshape(cow_int.shape), cmap="gray")
plt.title("Decompressed")
None
JPEG: Oblig 2 parafrase¶
Steg 1:¶
Last inn bilde

Steg 2:¶
Trekk fra 128
Steg 3:¶

Del opp i 8x8 blokker
Påfør 2D DCT på hver blokk: $$ F(u,v) = \frac{1}{4} c(u) c(v) \sum_{x=0}^{7} \sum_{y=0}^{7} f(x,y) \cos \bigg({\frac{(2x + 1)u\pi}{16}} \bigg) \cos \bigg({\frac{(2y + 1)v\pi}{16}} \bigg) $$ $$ c(a) = \frac{1}{\sqrt{2}} \hbox{ if a == 0 else 1} $$

$ Blokk(u,v) = \frac{1}{4} c(u) c(v) sum \Big($

*

$\Big) $
sampling = 32
cosinus = lambda x,u : np.cos( (2*x + 1)*u*np.pi / (sampling+sampling) )
cos_bilde = lambda u, v: [[ cosinus(x,u)*cosinus(y,v) for x in range(sampling)] for y in range(sampling)]
fig = plt.figure(figsize=(30,30))
for u in range(8):
for v in range(8):
cos_uv = cos_bilde(u,v)
fig.add_subplot(8,8,1+(u+v*8))
plt.imshow(cos_uv, cmap="gray")
plt.show()
Steg 4: Ikke faktisk en del av JPEG-algoritme, men en del av oblig¶
Rekonstruer med IDCT og +128 Test: Er før og etter lik? Da har du nok gjort det rett
Steg 5:¶

Fjerner: Psykovisuell redundans, i form av høye frekvenser
Del blokkene på qQ og rund av:

Steg 6:¶
Ting dere IKKE skal gjøre, men som er en del av JPEG:
- Indeks 0,0 (DC-komponenten) skal tas ut av hver blokk
- De resterende 63 pikslene i hver blokk skal bli representert mer kompakt
- DC-komponentene skal også transformeres til mer kompakt
- De kompakte representasjonene skal entropi-kodes (Huffman, Aritmetisk)
Det DERE skal: Regn ut
- Entropi
- Lagringsplass basert på entropi
- Kompresjonsrate
Steg 7:¶
Rekonstruer, og lagre til fil.
Bruk funksjonen på $$ q = [0.1,0.5,2,8,32] $$ Og svar på tekstsvarene!
Se forelesningen når den kommer ut! Lykke til med oblig :)¶