Litt om forrige forelesning: Kompresjon og koding II¶

Det som skal skje:¶

Differansetransform
Løpelengdetransform
Lempel-Ziv-Welch transform
Bittelitt om prediktiv koding

Denne gangen: Transform¶

Og intersampel redundans

Differansetransform¶

Utnytter at nabopiksler er like.

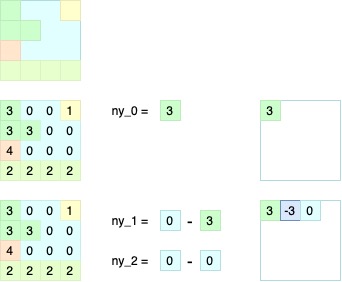
$$ ny_0 = img_0 $$$$ ny_1 = img_1 - img_0 $$$$ ny_n = img_n - img_{n-1} $$

Eksempel:

from imageio import imread; mona = imread("../images/lena.png", as_gray=True)
import numpy as np; new_mona = mona[:,1:mona.shape[1]]-mona[:,0:(mona.shape[1]-1)]
import matplotlib.pyplot as plt; plt.figure(figsize=(10,10)); plt.imshow(new_mona, cmap="gray"); plt.show()

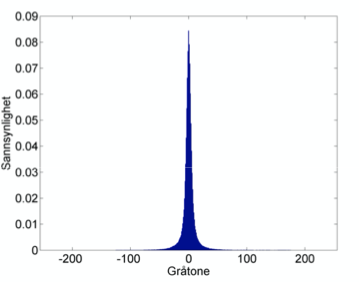
Verdiene sentreres rundt 0, og mange blir nå like. Lett å videre komprimere!

Løpelengdetransform¶

Sekvenser av like tall kan lagres som tallpar.

Eksempel: $$ \hbox{4444 555 7777} $$ Kan lagres som $$ \hbox{(4,4) (5,3) (7,4)} $$

Denne transformen sørger ofte for at videre koding er enklere.

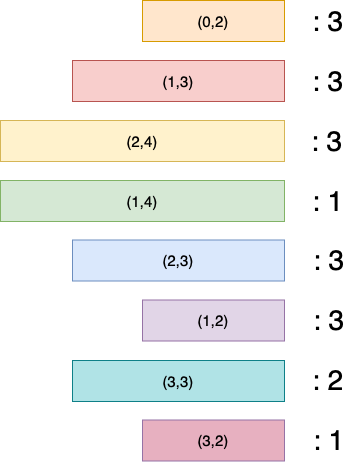
Eksempel: Ukeoppgave 2¶

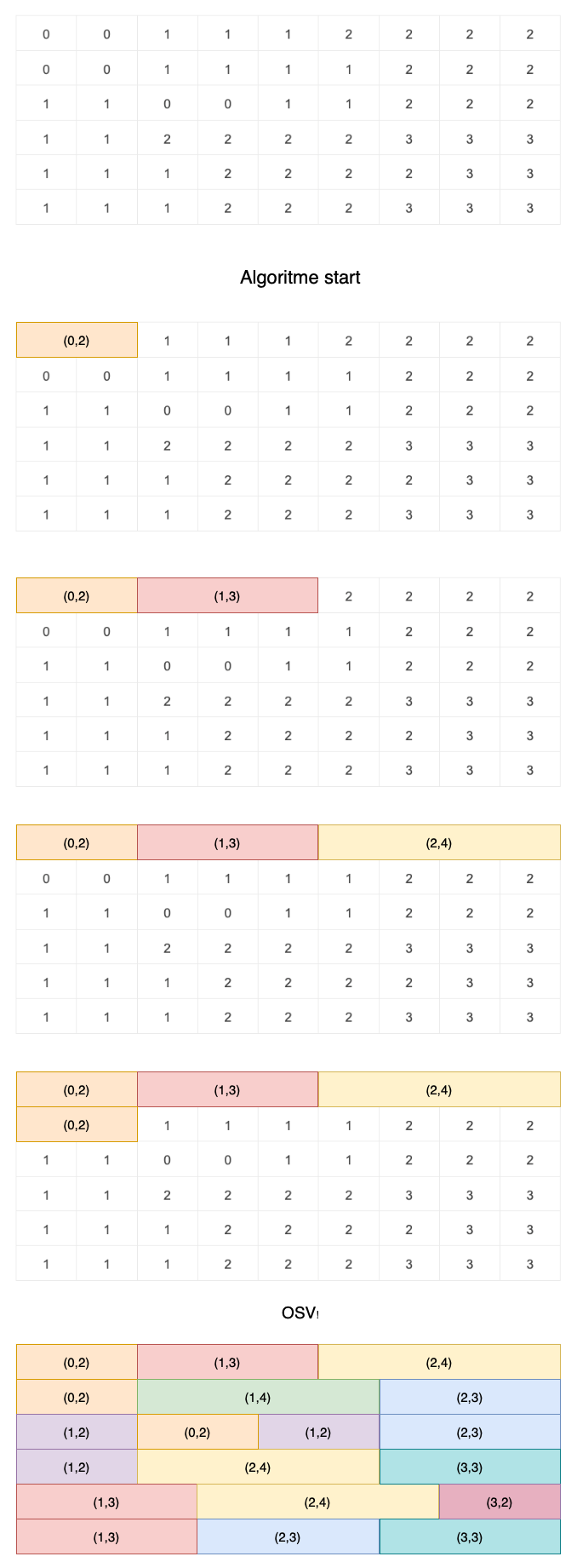
(0,2), (1,3), (2,4)
(0,2), (1,4), (2,3)
(1,2), (0,2), (1,2), (2,3)
(1,2), (2,4), (3,3)
(1,3), (2,4), (3,2)
(1,3), (2,3), (3,3)

Legg merke til at mange av tallparene forekommer mer enn en gang. Egnes til videre koding.

Lempel-Ziv-Welch¶

Transformerer en sekvens til en mindre sekvens basert på koder:

Init: Begge får startkodene
Kjører til tekst-slutt:
- Kod og send; motta og tolk
- Utvid lister

Eksempel: Fra forelesningen¶

Bittelitt om prediktiv koding¶

Prediktiv koding i 1D:¶

Tenk dere rekken: $$ \hbox{1 2 3 4 5 x} $$

Hva tror dere x er? Basert på de forrige sier vi 6.

$$ \hbox{1 2 3 4 5 7} $$

Vi vil lagre denne rekken etter feilene våre, om vi bruker formelen $ tall = forrige + 1 $:

$$ \hbox{0 0 0 0 0 1} $$

Jeg håper dere ser at denne lett kan Huffman-kodes!

Generelt:¶

I prediktiv koding "forutser" du den neste pikselen etter en formel, og lagrer feilen. Feilene kan lett entropikodes, fordi de, som differansetransformen, ofte er små.